968. 监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
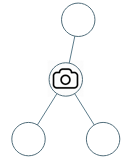
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
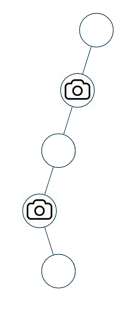
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是 [1, 1000]。
- 每个节点的值都是 0。
java代码
这是一道hard难度的题目。我们要从底向上进行推导,因为尽量让叶子节点的父节点安装摄像头,这样摄像头的数量才是最少的。 如何从低向上推导呢? 采用后序遍历也就是左右中的顺序,这样就可以从下到上进行推导了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
//NO_CAMERA表示的是子节点没有相机,当前节点也没放相机
private final int NO_CAMERA = 0;
//HAS_CAMERA表示当前节点有一个相机
private final int HAS_CAMERA = 1;
//NO_NEEDED表示当前节点没有相机,但他的子节点有一个相机,把它给
//覆盖了,所以它不需要了。或者他是一个空的节点也是不需要相机的
private final int NO_NEEDED = 2;
//全局的,统计有多少相机
int res = 0;
public int minCameraCover(TreeNode root) {
//边界条件判断
if (root == null)
return 0;
//如果最后返回的是NO_CAMERA,表示root节点的子节点也没有相机,
//所以root节点要添加一个相机
if (dfs(root) == NO_CAMERA)
res++;
//返回结果
return res;
}
public int dfs(TreeNode root) {
//如果是空的,就不需要相机了
if (root == null)
return NO_NEEDED;
int left = dfs(root.left);
int right = dfs(root.right);
//如果左右子节点有一个是NO_CAMERA,表示的是子节点既没相机,也没相机覆盖它,
//所以当前节点需要有一个相机
if (left == NO_CAMERA || right == NO_CAMERA) {
//在当前节点放一个相机,统计相机的个数
res++;
return HAS_CAMERA;
}
//如果左右子节点只要有一个有相机,那么当前节点就不需要相机了,否则返回一个没有相机的标记
return (left == HAS_CAMERA || right == HAS_CAMERA) ? NO_NEEDED : NO_CAMERA;
}
}
cpp代码
状态
- 0:该节点无覆盖,(说明,左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。)
- 1:本节点有摄像头
- 2:本节点有覆盖
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
//先考虑左右节点,再考虑中间节点,所以采用后序遍历
// 情况1 - - - - - - 左右节点都有覆盖
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;
// 情况2 - - - - - - - - - - - -- - - - 左右节点至少有一个无覆盖的情况
// left == 0 && right == 0 左右节点无覆盖
// left == 1 && right == 0 左节点有摄像头,右节点无覆盖
// left == 0 && right == 1 左节点有无覆盖,右节点摄像头
// left == 0 && right == 2 左节点无覆盖,右节点覆盖
// left == 2 && right == 0 左节点覆盖,右节点无覆盖
if (left == 0 || right == 0) {
result++;
return 1;
}
// 情况3 - - - - - - - - - - - - - - - - - - - - 左右节点至少有一个有摄像头
// left == 1 && right == 2 左节点有摄像头,右节点有覆盖
// left == 2 && right == 1 左节点有覆盖,右节点有摄像头
// left == 1 && right == 1 左右节点都有摄像头
// 其他情况前段代码均已覆盖
if (left == 1 || right == 1) return 2;
// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解
// 这个 return -1 逻辑不会走到这里。
return -1;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
// 情况4
if (traversal(root) == 0) { // root 无覆盖
result++;
}
return result;
}
};